清華新聞網(wǎng)9月11日電 在1950年的國際數(shù)學(xué)家大會(huì)上,克勞德·謝瓦萊(Claude Chevalley)提出了著名的謝瓦萊限制定理,即半單李代數(shù)上的共軛不變函數(shù)同構(gòu)于嘉當(dāng)子代數(shù)上的外爾群不變函數(shù)。該定理于1965年由羅伯特·施坦貝格(Robert Steinberg)完整證明,并推廣至半單代數(shù)群。此后,數(shù)學(xué)家們?cè)谥x瓦萊限制定理的高維推廣上取得了許多進(jìn)展:顏維諒(Gan Wee Liang)-維克多·金茨堡(Victor Ginzburg)、馬蒂亞斯·多莫科什(Matyas Domokos)、弗朗西斯科·瓦卡里諾(Francesco Vaccarino)解決了一般線性李代數(shù)的情形;陳朝銑(Chen Tsao-Hsien)-吳寶珠(Ngo Bao Chau)解決了辛李代數(shù)的情形;宋雷-夏曉朋-許金興解決了正交李代數(shù)的情形。
近日,清華大學(xué)丘成桐數(shù)學(xué)科學(xué)中心助理教授李鵬輝與美國加州大學(xué)伯克利分校教授戴維·納德勒(David Nadler)以及麻省理工學(xué)院教授惲之瑋合作,在幾何表示論與幾何朗蘭茲領(lǐng)域取得新進(jìn)展。團(tuán)隊(duì)在對(duì)仿射赫克范疇與交換堆的研究中取得重要的、原創(chuàng)性成果,并以“通過朗蘭茲對(duì)偶研究交換堆上的函數(shù)(Functions on the commuting stack via Langlands duality)”為題發(fā)表于9月出版的《數(shù)學(xué)年刊》(Annals of Mathematics)上。
李鵬輝與合作者一致性地證明了所有約化李代數(shù)和約化代數(shù)群的謝瓦萊定理的二維推廣。該問題解決的關(guān)鍵在于如何計(jì)算交換堆上的全局函數(shù)。團(tuán)隊(duì)創(chuàng)造性地運(yùn)用朗蘭茲對(duì)偶將其轉(zhuǎn)換成關(guān)于仿射赫克范疇余中心里的惠特克層的計(jì)算。由此,團(tuán)隊(duì)定義了該余中心的一個(gè)半正交分解,并使用特征層理論計(jì)算了每個(gè)分次塊,最終得到了描述惠特克層的自同態(tài)代數(shù),即交換堆上全局函數(shù)的公式。
在證明過程中,團(tuán)隊(duì)運(yùn)用范疇化收縮原理、拋物特征層理論、何-聶函數(shù)的梯度流、廣義斯普林格理論等多種理論,這些方法對(duì)于任意型的約化李代數(shù)、代數(shù)群均成立。謝瓦萊定理二維推廣的證明解決了數(shù)十年來關(guān)于交換堆的即約性猜想,對(duì)理解低維流形的朗蘭茲對(duì)偶有著重要意義。
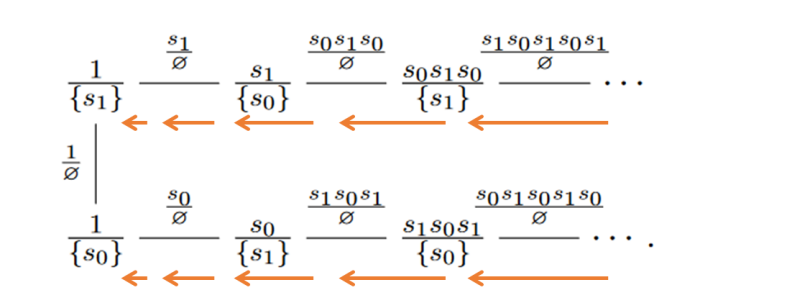
SL2時(shí)的何-聶函數(shù)梯度流
論文由李鵬輝、戴維·納德勒(David Nadler)、惲之瑋共同合作完成。研究得到中國國家自然科學(xué)基金、美國國家科學(xué)基金、西蒙斯學(xué)者獎(jiǎng)(Simons Investigatorship)與帕卡德獎(jiǎng)(Packard fellowship)的支持。
論文鏈接:
https://annals.math.princeton.edu/2024/200-2/p05
供稿:數(shù)學(xué)科學(xué)中心
題圖設(shè)計(jì):梁晨
編輯:李華山
審核:郭玲
