清華新聞網(wǎng)9月24日電 近日,清華大學(xué)丘成桐數(shù)學(xué)科學(xué)中心教授劉正偉,博士生邵鈺菓、魏付川,北京雁棲湖應(yīng)用數(shù)學(xué)研究院助理研究員程嵩提出了一種計(jì)算含噪聲量子線路期望值的高效方法——泡利基上的算符反向傳播(Observable's Back-propagation on Pauli Paths,OBPPP),這一變分量子算法在精度和速度上均優(yōu)于量子硬件,并可應(yīng)用于更廣泛類別的量子電路中。
目前,量子計(jì)算正處于所謂的“含噪聲中等規(guī)模量子硬件時(shí)代(NISQ Era)”。變分量子算法憑借其對(duì)量子硬件更低的要求,有望率先實(shí)現(xiàn)可應(yīng)用且有意義的量子算法,因而在組合優(yōu)化、量子化學(xué)、材料計(jì)算乃至機(jī)器學(xué)習(xí)等領(lǐng)域都備受關(guān)注。但變分量子算法的研究仍面臨著諸多難題,如線路噪聲帶來的退相干、表達(dá)能力的局限、可訓(xùn)練性的喪失等。事實(shí)上,找到相對(duì)經(jīng)典且真正具備量子優(yōu)勢(shì)的變分量子算法,依舊是一個(gè)科學(xué)界反復(fù)討論又難以解決的開放問題。一個(gè)同樣重要的反問題是:什么類型的變分量子算法是容易被經(jīng)典模擬的?
數(shù)學(xué)中心量子對(duì)稱團(tuán)隊(duì)從理論上證明了一大類常見的變分量子算法,其架構(gòu)均不具有量子優(yōu)勢(shì)。基于這一理論,團(tuán)隊(duì)創(chuàng)造性地構(gòu)建了一個(gè)切實(shí)可算的多項(xiàng)式復(fù)雜度的經(jīng)典算法——OBPPP,并與上述變分量子算法進(jìn)行對(duì)比,獲得了喜人的結(jié)果。
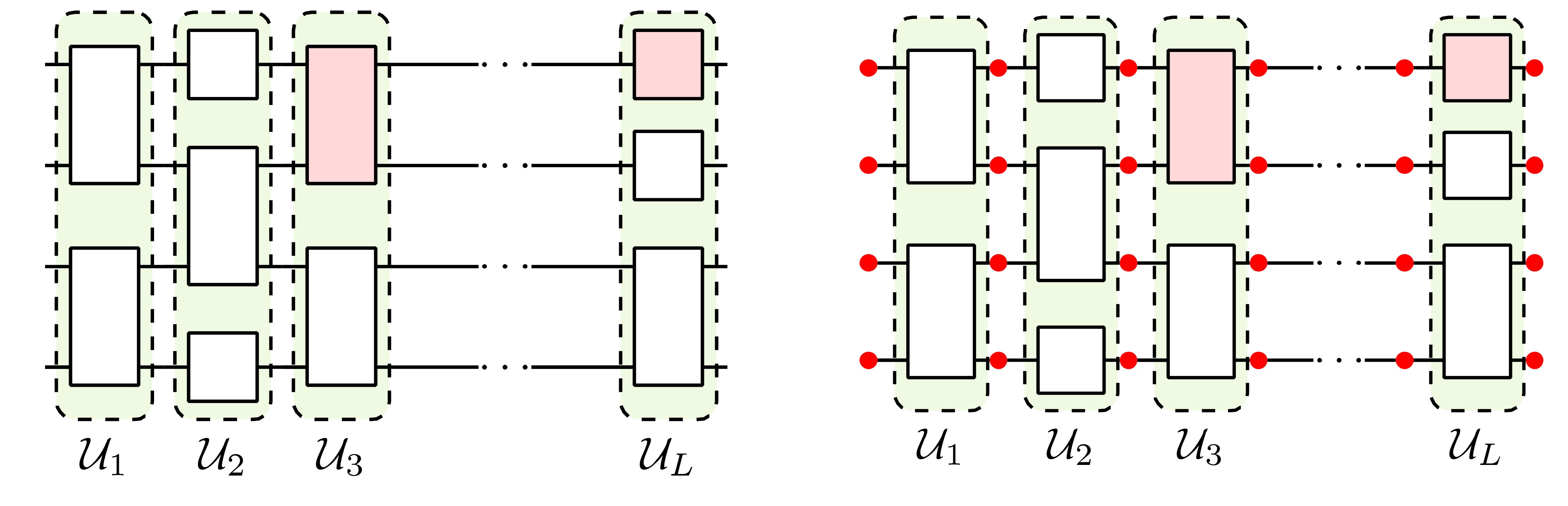
左:無噪聲量子線路示意圖 右:含噪聲量子線路示意圖
該工作考察了由Clifford門與任意比特單參數(shù)Pauli旋轉(zhuǎn)門共同組成的量子線路(上圖分別對(duì)應(yīng)白色和粉色方塊表示),囊括了當(dāng)前大部分變分量子算法的線路架構(gòu)。同時(shí)考慮線路中存在獨(dú)立的單比特Pauli型噪聲通道,這一噪聲模型包括了實(shí)驗(yàn)中最常見的去極化噪聲(depolarizing)和退相位噪聲(dephasing)等。研究團(tuán)隊(duì)認(rèn)為,同樣的方法也可以很容易地推廣至更普遍的單比特噪聲,比如保單位噪聲(unital noise)。
對(duì)于上述常見的變分量子線路架構(gòu),研究人員發(fā)現(xiàn)在Pauli基上將整個(gè)線路進(jìn)行傅里葉展開,觀測(cè)算符在線路上的期望值,表達(dá)為在Pauli基上的路徑積分,可以大幅度提高現(xiàn)有經(jīng)典算法對(duì)于變分量子算法的模擬速度。這一方法有兩個(gè)顯著的好處,其一,由Clifford門與任意比特單參數(shù)Pauli旋轉(zhuǎn)門組成的量子線路在此展開下性質(zhì)良好,展開的項(xiàng)數(shù)往往少于傳統(tǒng)算法(例如張量網(wǎng)絡(luò)方法中的求和項(xiàng),狀態(tài)矢量state vector方法中的計(jì)算基項(xiàng));其二,在Pauli型噪聲參與的情況下,大量路徑的貢獻(xiàn)受到壓制且壓制系數(shù)具有清楚的表達(dá)式:

這保證了有限數(shù)值精度的前提下,能夠做到算法復(fù)雜度僅隨量子線路深度與量子比特?cái)?shù)多項(xiàng)式增長(zhǎng)。
研究人員在理論上證明了這類含噪聲量子線路算符期望的經(jīng)典可模擬性。他們發(fā)現(xiàn)全體Pauli型噪聲可以分為兩種情形,保持一個(gè)固定的截?cái)嗾`差,各自證明了兩種情形下經(jīng)典模擬的時(shí)間復(fù)雜度為:
情形一:
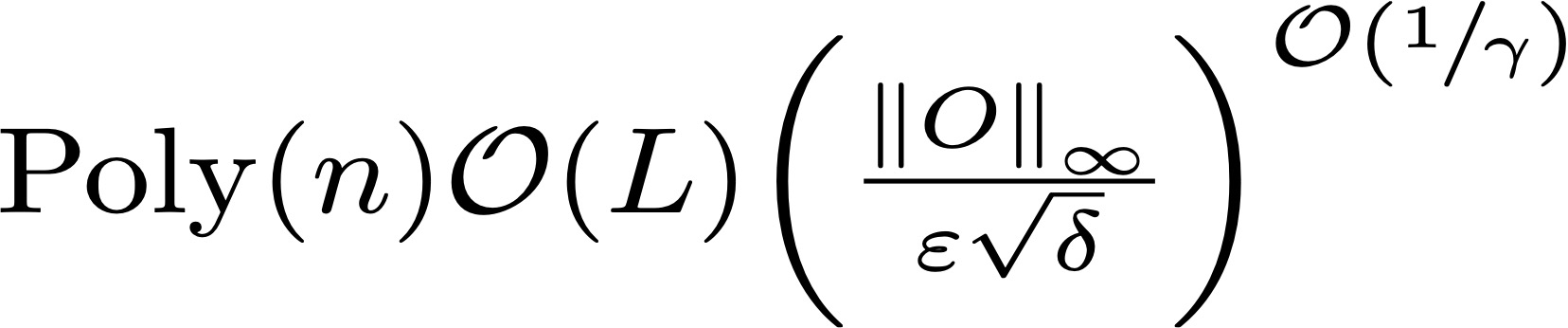
情形二:
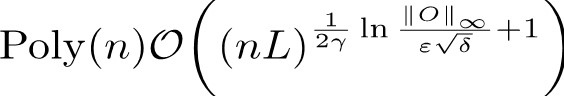
其中n為比特?cái)?shù),L為深度,Epsilon為數(shù)值誤差,Gamma為噪聲率。事實(shí)上,在常數(shù)非零噪聲率下,OBPPP的時(shí)間和空間復(fù)雜度與量子比特?cái)?shù)n和電路深度L均呈多項(xiàng)式關(guān)系。在一般的線路中通常為指數(shù)關(guān)系。
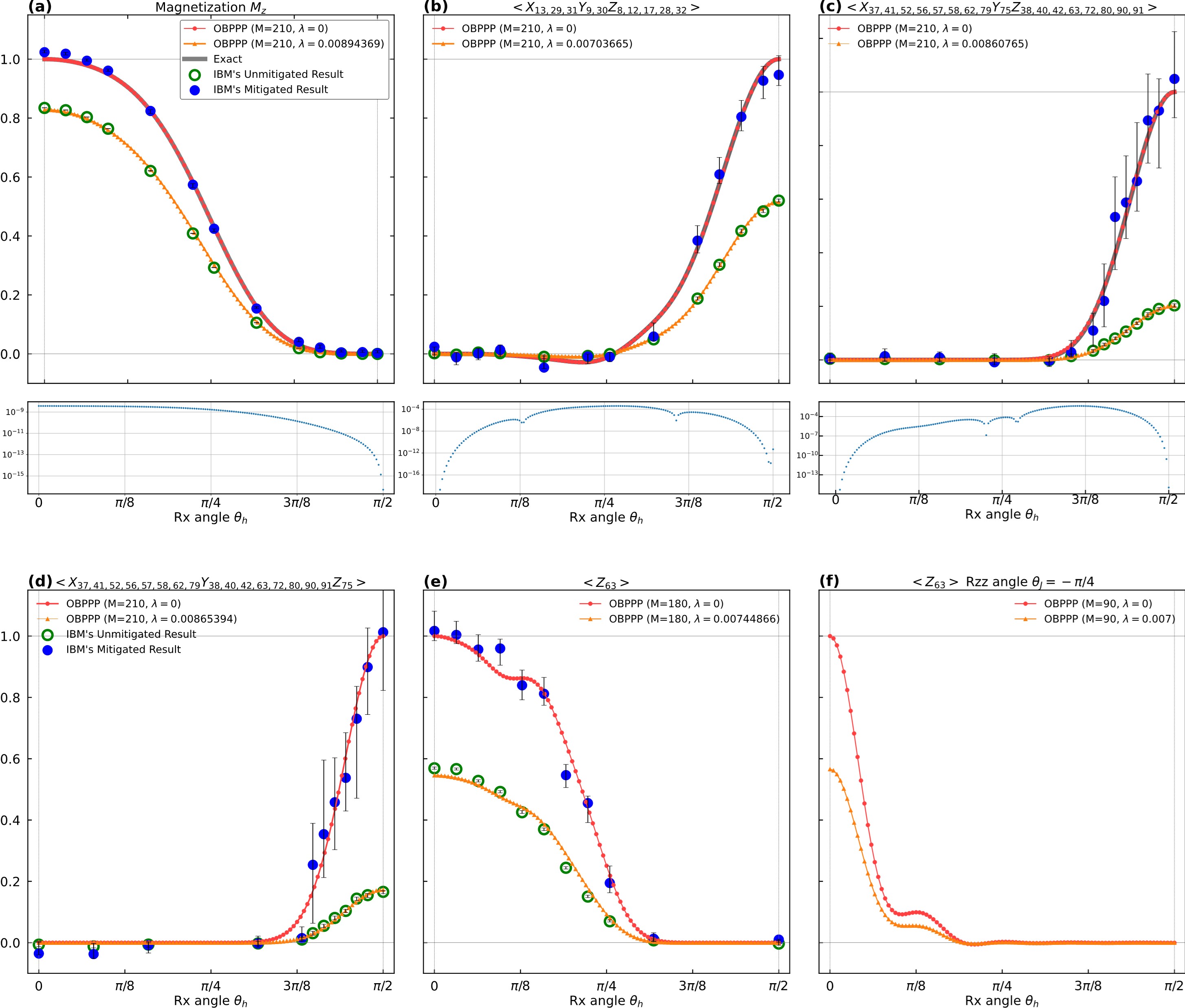
模擬結(jié)果與IBM Eagle量子處理器的實(shí)驗(yàn)結(jié)果高度吻合
研究人員成功地對(duì)IBM的Eagle量子處理器的算法進(jìn)行了經(jīng)典模擬,運(yùn)行時(shí)間比量子硬件更短,同時(shí)實(shí)現(xiàn)了更準(zhǔn)確的期望值。以模擬IBM算法實(shí)驗(yàn)為例,量子比特?cái)?shù)為127,線路深度為80,OBPPP得到每張圖的計(jì)算時(shí)間均小于5分鐘(基于2張Xeon6330 CPU的結(jié)果)。此外,對(duì)不同的噪聲率,根據(jù)路徑壓制因子,從而很容易地推出對(duì)應(yīng)算符期望值,與未修正的原始實(shí)驗(yàn)數(shù)據(jù)直接對(duì)比,表現(xiàn)出與實(shí)驗(yàn)結(jié)果很強(qiáng)的一致性。
研究針對(duì)含單比特Pauli型噪聲的變分量子線路,考慮線路由Clifford門與任意比特單參數(shù)Pauli旋轉(zhuǎn)門組成。研究人員發(fā)現(xiàn),OBPPP能夠?qū)崿F(xiàn)此線路下算符期望值的高效近似,并保證有界的截?cái)嗾`差。研究團(tuán)隊(duì)在理論上證明了存在常數(shù)非零噪聲率時(shí),OBPPP的時(shí)間和空間復(fù)雜度與量子比特?cái)?shù)n和電路深度L均呈多項(xiàng)式關(guān)系。數(shù)值上,通過對(duì)IBM 127量子比特Eagle處理器的經(jīng)典模擬,驗(yàn)證了該方法在精度和運(yùn)行速度上均優(yōu)于量子硬件,能夠準(zhǔn)確模擬還原噪聲影響下的實(shí)驗(yàn)結(jié)果。此外,該工作還細(xì)致地揭示了噪聲與經(jīng)典可模擬性的關(guān)系,展示了該方法在更廣泛類別的量子電路中的適用性。
9月18日,相關(guān)研究成果以“模擬含噪聲變分量子算法:一種多項(xiàng)式途徑”(Simulating Noisy Variational Quantum Algorithms: A Polynomial Approach)為題,發(fā)表于《物理評(píng)論快報(bào)》(Physical Review Letters)。
清華大學(xué)丘成桐數(shù)學(xué)科學(xué)中心與北京雁棲湖應(yīng)用數(shù)學(xué)研究院共同完成這項(xiàng)工作。論文第一作者為數(shù)學(xué)中心2020級(jí)博士生邵鈺菓。劉正偉、程嵩為論文通訊作者。數(shù)學(xué)中心2021級(jí)博士生魏付川參與合作。
論文鏈接:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.120603#fulltext
供稿:數(shù)學(xué)科學(xué)中心
題圖設(shè)計(jì):李柳依
編輯:李華山
審核:郭玲
